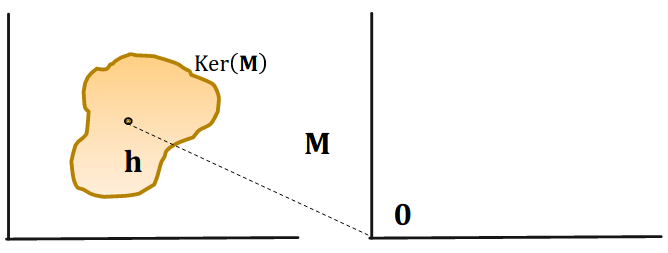This post based on 10. Knowledge Graph Embeddings of CS224W
Knowledge Graphs# Knowledge in graph form:
Capture entities, types, and relationships
Nodes are entities
Nodes are labeled with their types
Edges between two nodes capture relationships between entities
Knowledge Graph (KG) is an example of a heterogeneous graph
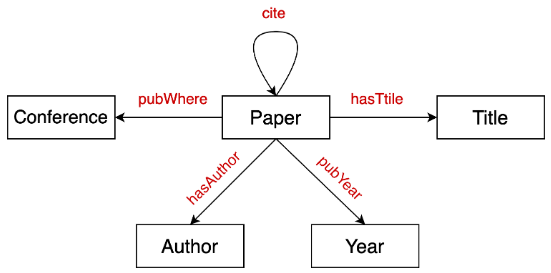
Bibliographic Networks
Node types: paper, title, author, conference, year
Relation types: pubWhere, pubYear, hasTitle, hasAuthor, cite
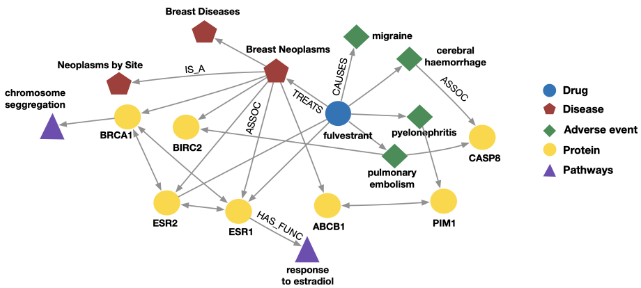
Bio Knowledge Graphs
Node types: drug, disease, adverse event, protein, pathways
Relation types: has_func, causes, assoc, treats, is_a
Examples of knowledge graphs:
Google Knowledge Graph
Amazon Product Graph
Facebook Graph API
IBM Watson
Microsoft Satori
Project Hanover/Literome
LinkedIn Knowledge Graph
Yandex Object Answer
Building a Knowledge Graph-based Dialogue System at the 2nd ConvAI Summer School
Datasets# Publicly available KGs:
FreeBase, Wikidata, Dbpedia, YAGO, NELL, etc.
Common characteristics:
enumerating all the possible facts is intractable!
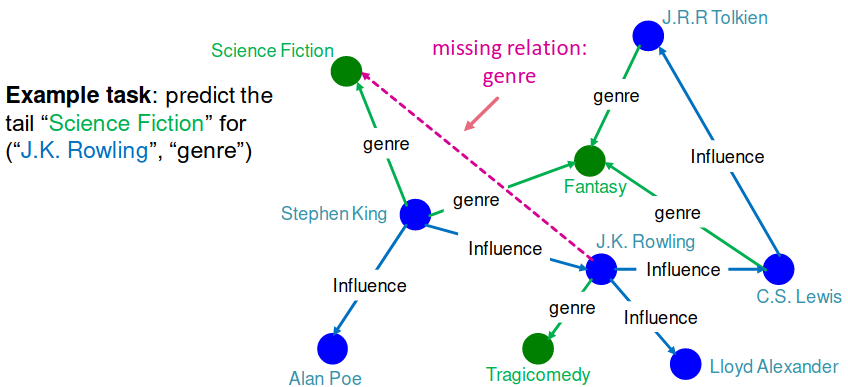
Given an enormous KG, can we complete the KG?
For a given (head, relation), we predict missing tails.
(Note this is slightly different from link prediction task)
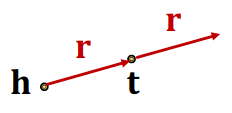
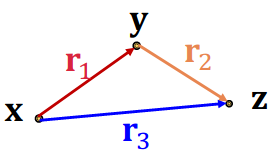
KG Representation# Edges in KG are represented as triples ( h , r , t ) (h, r, t) ( h , r , t )
head (h h h r r r t t t
Key Idea :
Model entities and relations in the embedding/vector space R d {\Bbb R}^d R d
Associate entities and relations with shallow embeddings
Note we do not learn a GNN here!
Given a true triple ( h , r , t ) (h, r, t) ( h , r , t ) ( h , r ) (h, r) ( h , r ) t t t
How to embed ( h , r ) (h, r) ( h , r )
How to define closeness?
We are going to learn about different KG embedding models (shallow/transductive embs):
Different models are…
…based on different geometric intuitions
…capture different types of relations (have different expressivity)
Relations:#
Symmetric Relation
Antisymmetric Relation
Inverse Relation
Composition (Transitive) Relation
1-to-N Relation
TransE# https://papers.nips.cc/paper/2013/hash/1cecc7a77928ca8133fa24680a88d2f9-Abstract.html
Translation Intuition:
For a triple ( h , r , t ) (h, r, t) ( h , r , t ) h , r , t ∈ R d \bf{h, r, t} \in {\Bbb R}^d h , r , t ∈ R d h + r ≈ t \bf{h + r \approx t} h + r ≈ t h + r ≠ t \bf{h + r \neq t} h + r = t
Scoring function: f r ( h , t ) = − ∥ h + r − t ∥ f_r (h,t) = -\| \bf{h + r - t} \| f r ( h , t ) = − ∥ h + r − t ∥
Relations in a heterogeneous KG have different properties:
Example:
Symmetry: If the edge (h h h t t t t t t h h h
Inverse relation: If the edge (h h h t t t t t t h h h
Can we categorize these relation patterns?
Are KG embedding methods (e.g., TransE) expressive enough to model these patterns?
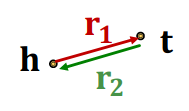
Antisymmetric Relations:# r ( h , t ) ⇒ ¬ r ( t , h ) , ∀ h , t r(h,t) \rArr \neg r(t,h),\ \forall h,t r ( h , t ) ⇒ ¬ r ( t , h ) , ∀ h , t
Antisymmetric: Hypernym
h + r = t \bf{h + r = t} h + r = t t + r ≠ h \bf{t + r \neq h} t + r = h
Inverse Relations:# r 2 ( h , t ) ⇒ r 1 ( t , h ) r_2 (h,t) \rArr r_1 (t,h) r 2 ( h , t ) ⇒ r 1 ( t , h )
Example : (Advisor, Advisee)
h + r 2 = t \bf{h + r_{\rm 2} = t} h + r 2 = t r 1 = − r 2 \bf{r}_1 = -\bf{r}_2 r 1 = − r 2
Composition (Transitive) Relations:# r 1 ( x , y ) ∧ r 2 ( y , z ) ⇒ r 3 ( x , z ) , ∀ x , y , z r_1 (x,y) \land r_2 (y,z) \rArr r_3 (x, z),\ \forall x, y, z r 1 ( x , y ) ∧ r 2 ( y , z ) ⇒ r 3 ( x , z ) , ∀ x , y , z
Example: My mother’s husband is my father.
r 3 = r 1 + r 2 \bf{r}_3 = \bf{r}_1 + \bf{r}_2 r 3 = r 1 + r 2
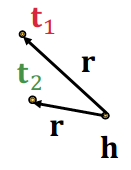
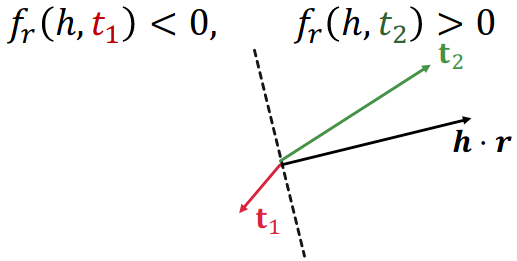
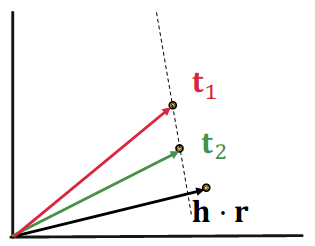
1-to-N relations:# r ( h , t 1 ) , r ( h , t 2 ) , … , r ( h , t n ) r(h, t_1), r(h, t_2), …, r(h, t_n) r ( h , t 1 ) , r ( h , t 2 ) , … , r ( h , t n )
Example: ( h , r , t 1 ) (h, r, t_1) ( h , r , t 1 ) ( h , r , t 2 ) (h, r, t_2) ( h , r , t 2 ) r r r
TransE cannot model 1-to-N relations; t 1 \bf{t}_1 t 1 t 2 \bf{t}_2 t 2
t 1 = h + r = t 2 \bf{t}_1 = \bf{h + r} = \bf{t}_2 t 1 = h + r = t 2 t 1 ≠ t 2 \bf{t}_1 \neq \bf{t}_2 t 1 = t 2
Symmetric relations# r ( h , t ) ⇒ r ( t , h ) , ∀ h , t r(h,t) \rArr r(t, h),\ \forall h,t r ( h , t ) ⇒ r ( t , h ) , ∀ h , t
Example: Family, Roommate
TransE cannot model symmetric relations
only if r = 0 , h = t \bf{r} = 0, \bf{h = t} r = 0 , h = t
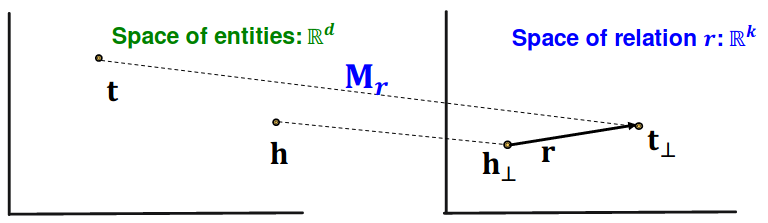
TransR# Learning Entity and Relation Embeddings for Knowledge Graph Completion
TransE models translation of any relation in the same embedding space.
Can we design a new space for each relation and do translation in relation-specific space?
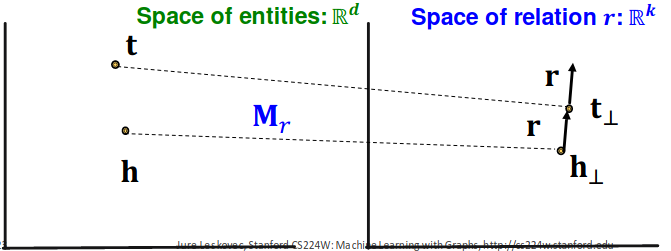
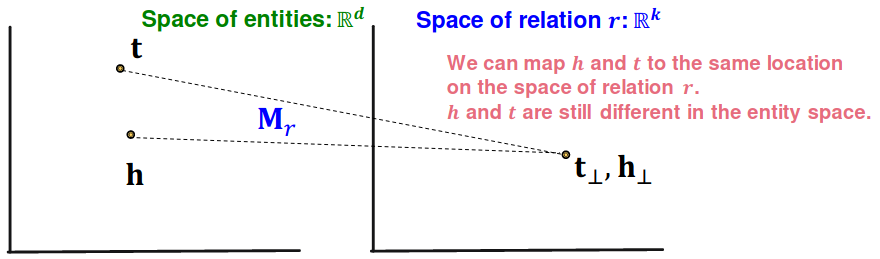
TransR: model entities as vectors in the entity space ℝ𝑑 and model each relation as vector in relation space r ∈ R k {\bf r} \in \Bbb{R}^k r ∈ R k M r ∈ R k × d {\bf M}_r \in {\Bbb R}^{k\times d} M r ∈ R k × d
h ⊥ = M r h {\bf h}_\perp = {\bf M}_r {\bf h} h ⊥ = M r h t ⊥ = M r t {\bf t}_\perp = {\bf M}_r {\bf t} t ⊥ = M r t
Score function: f r ( h , t ) = − ∥ h ⊥ + r − t ⊥ ∥ f_r (h,t) = -\| \bf{h_\perp + r - t_\perp} \| f r ( h , t ) = − ∥ h ⊥ + r − t ⊥ ∥
Mark
Specifically, in the equation h ⊥ = M r h {\bf h}_\perp = {\bf M}_r {\bf h} h ⊥ = M r h h ⊥ {\bf h}_\perp h ⊥ h {\bf h} h M {\bf M} M ⊥ \perp ⊥ to distinguish this vector from other vectors that may be used in the context of the equation.
In general mathematical notation, the symbol ⊥ \perp ⊥ ⊥ \perp ⊥ ⊥ \perp ⊥
Note different symmetric relations may have different M r {\bf M}_r M r
Symmetric relations:# r ( h , t ) ⇒ r ( t , h ) , ∀ h , t r(h,t) \rArr r(t, h),\ \forall h,t r ( h , t ) ⇒ r ( t , h ) , ∀ h , t
Example: Family, Roommate
TransR can model symmetric relations
r = 0 , h ⊥ = M r h = M r t = t ⊥ {\bf r}=0,\ {\bf h}_\perp = {\bf M}_r {\bf h} = {\bf M}_r {\bf t} = {\bf t}_\perp r = 0 , h ⊥ = M r h = M r t = t ⊥
Antisymmetric relations:#
TransR can model antisymmetric relations
r ≠ 0 , M r h + r = M r t {\bf r} \neq 0,\ {\bf M}_r {\bf h} + {\bf r} = {\bf M}_r {\bf t} r = 0 , M r h + r = M r t M r t + r ≠ M r h {\bf M}_r {\bf t} + {\bf r} \neq {\bf M}_r {\bf h} M r t + r = M r h
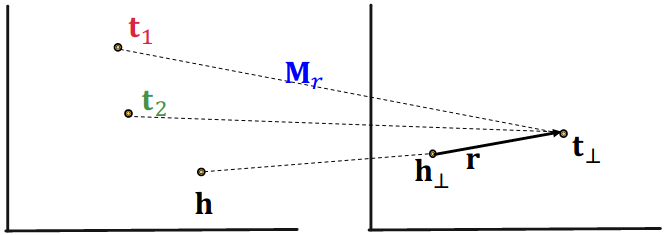
1-to-N Relations:# r ( h , t 1 ) , r ( h , t 2 ) , … , r ( h , t n ) r(h, t_1), r(h, t_2), …, r(h, t_n) r ( h , t 1 ) , r ( h , t 2 ) , … , r ( h , t n )
TransR can model 1-to-N relations
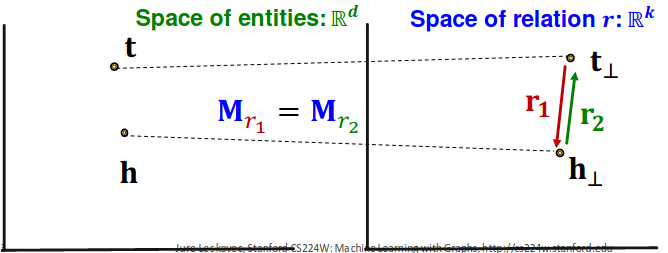
Inverse Relations:#
TransR can model inverse relations
r 2 = − r 1 {\bf r}_2 = -{\bf r}_1 r 2 = − r 1 M r 1 = M r 2 {\bf M}_{r_1} = {\bf M}_{r_2} M r 1 = M r 2 M r 1 t + r 1 = M r 1 h {\bf M}_{r_1} {\bf t} + {\bf r}_1 = {\bf M}_{r_1} {\bf h} M r 1 t + r 1 = M r 1 h M r 2 h + r 2 = M r 2 t {\bf M}_{r_2} {\bf h} + {\bf r}_2 = {\bf M}_{r_2} {\bf t} M r 2 h + r 2 = M r 2 t
Composition Relations:#
TransR can model composition relations
High-level intuition: TransR models a triple with linear functions, they are chainable.
Assume M r a g a = r a {\bf M}_{r_a} {\bf g}_a = {\bf r}_a M r a g a = r a M r b g b = r b {\bf M}_{r_b} {\bf g}_b = {\bf r}_b M r b g b = r b
For r 1 ( x , y ) r_1(x, y) r 1 ( x , y )
M r 1 x + r 1 = M r 1 y → y − x ∈ g 1 + Ker ( M r 1 ) → y ∈ x + g 1 + Ker ( M r 1 ) \begin{aligned}
&{\bf M}_{r_1} {\bf x} + {\bf r}_1 = {\bf M}_{r_1} {\bf y} \rarr\\
&{\bf y - x} \in {\bf g}_1 + \text{Ker}({\bf M}_{r_1}) \rarr\\
&{\bf y} \in {\bf x} + {\bf g}_1 + \text{Ker}({\bf M}_{r_1})
\end{aligned} M r 1 x + r 1 = M r 1 y → y − x ∈ g 1 + Ker ( M r 1 ) → y ∈ x + g 1 + Ker ( M r 1 ) For r 2 ( y , z ) r_2(y, z) r 2 ( y , z )
M r 2 y + r 2 = M r 2 z → z − y ∈ g 2 + Ker ( M r 2 ) → z ∈ y + g 2 + Ker ( M r 2 ) \begin{aligned}
&{\bf M}_{r_2} {\bf y} + {\bf r}_2 = {\bf M}_{r_2} {\bf z} \rarr\\
&{\bf z - y} \in {\bf g}_2 + \text{Ker}({\bf M}_{r_2}) \rarr\\
&{\bf z} \in {\bf y} + {\bf g}_2 + \text{Ker}({\bf M}_{r_2})
\end{aligned} M r 2 y + r 2 = M r 2 z → z − y ∈ g 2 + Ker ( M r 2 ) → z ∈ y + g 2 + Ker ( M r 2 ) Then,
z ∈ x + g 1 + g 2 + Ker ( M r 1 ) + Ker ( M r 2 ) {\bf z} \in {\bf x} + {\bf g}_1 + {\bf g}_2+ \text{Ker}({\bf M}_{r_1}) + \text{Ker}({\bf M}_{r_2}) z ∈ x + g 1 + g 2 + Ker ( M r 1 ) + Ker ( M r 2 ) Construct M r 3 {\bf M}_{r_3} M r 3 Ker ( M r 3 ) = Ker ( M r 1 ) + Ker ( M r 2 ) \text{Ker}({\bf M}_{r_3}) = \text{Ker}({\bf M}_{r_1}) + \text{Ker}({\bf M}_{r_2}) Ker ( M r 3 ) = Ker ( M r 1 ) + Ker ( M r 2 )
Since,dim ( Ker ( M r 3 ) ) ≥ dim ( Ker ( M r 1 ) ) \text{dim}\left(\text{Ker}({\bf M}_{r_3})\right) \ge \text{dim}\left(\text{Ker}({\bf M}_{r_1})\right) dim ( Ker ( M r 3 ) ) ≥ dim ( Ker ( M r 1 ) ) M r 3 {\bf M}_{r_3} M r 3 M r 1 {\bf M}_{r_1} M r 1
We know M r 3 {\bf M}_{r_3} M r 3
Set r 3 = M r 3 ( g 1 + g 2 ) {\bf r}_3 = {\bf M}_{r_3}({\bf g}_1 + {\bf g}_2) r 3 = M r 3 ( g 1 + g 2 )
We are done! We have M r 3 x + r 3 = M r 3 z {\bf M}_{r_3} {\bf x} + {\bf r}_3 = {\bf M}_{r_3} {\bf z} M r 3 x + r 3 = M r 3 z
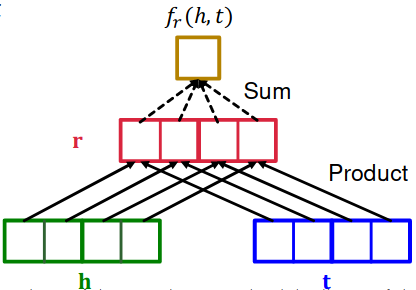
DistMult# Embedding Entities and Relations for Learning and Inference in Knowledge Bases
https://arxiv.org/abs/1412.6575
Mark
The idea is that the DistMult model learns to place the hyperplanes
maximizes the similarity between the heads and tails of known triples
minimizing the similarity between the heads and tails of incorrect triples
This allows the model to make accurate predictions about the missing element in a given triple.
In DistMult, each (head, relation) pair is represented by a hyperplan , which is a geometric object that can be thought of as a flat, n-dimensional surface that divides a space into two regions. The hyperplane is defined by a set of parameters that determine its orientation and position in the space.
Mark
In the context of knowledge representation and reasoning, a “triple” typically refers to a statement in the form of (subject , relation , object ), where the relation is the predicate that connects the subject and object entities.
For example, in the knowledge graph of movies, a triple might be (The Matrix, hasGenre, Action). In this triple, “The Matrix” is the subject, “hasGenre” is the relation, and “Action” is the object.
The scoring function f r ( h , t ) f_r(h, t) f r ( h , t )
Entities and relations using vectors in R k {\Bbb R}^k R k
Score function: f r ( h , t ) = < h , r , t > = ∑ i h i ⋅ r i ⋅ t i , h , r , t ∈ R k f_r(h, t) = < {\bf h}, {\bf r}, {\bf t} > = \sum_i {\bf h}_i \cdot {\bf r}_i \cdot {\bf t}_i,\quad {\bf h}, {\bf r}, {\bf t} \in {\Bbb R}^k f r ( h , t ) =< h , r , t >= ∑ i h i ⋅ r i ⋅ t i , h , r , t ∈ R k
Bilinear modeling
Intuition of the score function: Can be viewed as a cosine similarity between h ⋅ r {\bf h} \cdot {\bf r} h ⋅ r t {\bf t} t
1-to-N Relations:# r ( h , t 1 ) , r ( h , t 2 ) , … , r ( h , t n ) r(h, t_1), r(h, t_2), …, r(h, t_n) r ( h , t 1 ) , r ( h , t 2 ) , … , r ( h , t n )
< h , r , t 1 > = < h , r , t 2 > < {\bf h}, {\bf r}, {\bf t}_1 > = < {\bf h}, {\bf r}, {\bf t}_2 > < h , r , t 1 >=< h , r , t 2 >
Symmetric Relations:# r ( h , t ) ⇒ r ( t , h ) , ∀ h , t r(h,t) \rArr r(t, h),\ \forall h,t r ( h , t ) ⇒ r ( t , h ) , ∀ h , t
f r ( h , t ) = < h , r , t > = ∑ i h i ⋅ r i ⋅ t i = < t , r , h > = f r ( t , h ) f_r(h, t) = < {\bf h}, {\bf r}, {\bf t} > = \sum_i {\bf h}_i \cdot {\bf r}_i \cdot {\bf t}_i = < {\bf t}, {\bf r}, {\bf h} > = f_r(t, h) f r ( h , t ) =< h , r , t >= ∑ i h i ⋅ r i ⋅ t i =< t , r , h >= f r ( t , h )
Then, r ( h , t ) r(h, t) r ( h , t ) r ( t , h ) r(t, h) r ( t , h ) Antisymmetric relations
Also, Inverse relations not possible.
f r 2 ( h , t ) = < h , r 2 , t > = < t , r 1 , h > = f r 1 ( t , h ) f_{r_2}(h, t) = < {\bf h}, {\bf r}_2, {\bf t} > = < {\bf t}, {\bf r}_1, {\bf h} > = f_{r_1}(t, h) f r 2 ( h , t ) =< h , r 2 , t >=< t , r 1 , h >= f r 1 ( t , h )
This mean r 2 = r 1 {r_2} = {r_1} r 2 = r 1
But semantically this does not make sense: The embedding of “Advisor” should not be the same with “Advisee”.
Composition relations:# r 1 ( x , y ) ∧ r 2 ( y , z ) ⇒ r 3 ( x , z ) , ∀ x , y , z r_1 (x,y) \land r_2 (y,z) \rArr r_3 (x, z),\ \forall x, y, z r 1 ( x , y ) ∧ r 2 ( y , z ) ⇒ r 3 ( x , z ) , ∀ x , y , z
Mark
To understand this limitation, it may be helpful to think of the hyperplane as a boundary that separates two regions of the space. When two relations are combined in a multi-hop path, the resulting boundary is more complex and may not be able to be represented by a single hyperplane. This means that the DistMult model may not be able to learn the correct relationship between the head and tail of the triple in these cases, and may make inaccurate predictions.
This dot product can be thought of as a projection of the head vector onto a hyperplane defined by the relation vector.
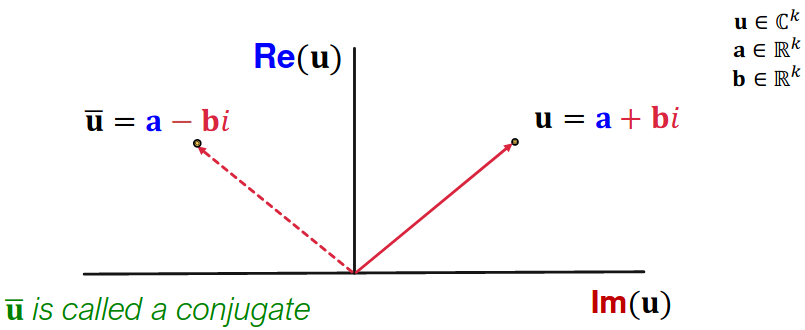
ComplEx# Trouillon et al, Complex Embeddings for Simple Link Prediction , ICML 2016
Based on Distmult, ComplEx embeds entities and relations in Complex vector space
ComplEx: model entities and relations using vectors in C k {\Bbb C}^k C k
Imaginary: 허수
Score function: f r ( h , t ) = Re ( ∑ i h i ⋅ r i ⋅ t ˉ i ) f_r(h, t) = \text{Re}(\sum_i {\bf h}_i \cdot {\bf r}_i \cdot {\bf \bar{t}}_i) f r ( h , t ) = Re ( ∑ i h i ⋅ r i ⋅ t ˉ i )
Antisymmetric Relations:#
The model is expressive enough to learn
High, f r ( h , t ) = Re ( ∑ i h i ⋅ r i ⋅ t ˉ i ) f_r(h, t) = \text{Re}(\sum_i {\bf h}_i \cdot {\bf r}_i \cdot {\bf \bar{t}}_i) f r ( h , t ) = Re ( ∑ i h i ⋅ r i ⋅ t ˉ i )
Low, f r ( t , h ) = Re ( ∑ i t i ⋅ r i ⋅ h ˉ i ) f_r(t, h) = \text{Re}(\sum_i {\bf t}_i \cdot {\bf r}_i \cdot {\bf \bar{h}}_i) f r ( t , h ) = Re ( ∑ i t i ⋅ r i ⋅ h ˉ i )
Due to the asymmetric modeling using complex conjugate.
Symmetric Relations:# r ( h , t ) ⇒ r ( t , h ) , ∀ h , t r(h,t) \rArr r(t, h),\ \forall h,t r ( h , t ) ⇒ r ( t , h ) , ∀ h , t
When Im ( r ) = 0 \text{Im}({\bf r}) = 0 Im ( r ) = 0
f r ( h , t ) = Re ( ∑ i h i ⋅ r i ⋅ t ˉ i ) = ∑ i Re ( r i ⋅ h i ⋅ t ˉ i ) = ∑ i r i ⋅ Re ( ⋅ h i ⋅ t ˉ i ) = ∑ i r i ⋅ Re ( ⋅ h ˉ i ⋅ t i ) = ∑ i Re ( r i ⋅ h ˉ i ⋅ t i ) = f r ( t , h ) \begin{aligned}
f_r(h, t) &= \text{Re}(\sum_i {\bf h}_i \cdot {\bf r}_i \cdot {\bf \bar{t}}_i)\\
&= \sum_i \text{Re}({\bf r}_i \cdot {\bf h}_i \cdot {\bf \bar{t}}_i) \\
&= \sum_i {\bf r}_i \cdot \text{Re}( \cdot {\bf h}_i \cdot {\bf \bar{t}}_i) \\
&= \sum_i {\bf r}_i \cdot \text{Re}( \cdot {\bf \bar{h}}_i \cdot {\bf t}_i) \\
&= \sum_i \text{Re}( {\bf r}_i \cdot {\bf \bar{h}}_i \cdot {\bf t}_i) = f_r(t, h)
\end{aligned} f r ( h , t ) = Re ( i ∑ h i ⋅ r i ⋅ t ˉ i ) = i ∑ Re ( r i ⋅ h i ⋅ t ˉ i ) = i ∑ r i ⋅ Re ( ⋅ h i ⋅ t ˉ i ) = i ∑ r i ⋅ Re ( ⋅ h ˉ i ⋅ t i ) = i ∑ Re ( r i ⋅ h ˉ i ⋅ t i ) = f r ( t , h ) Inverse Relations:#
r = r ˉ 2 {\bf r} = {\bf \bar{r}}_2 r = r ˉ 2 r 2 = arg max r Re ( < h , r , t ˉ > ) = arg max r Re ( < t , r , h ˉ > ) = r 1 {\bf r}_2 = \argmax\limits_r \text{Re}(<{\bf h}, {\bf r}, {\bf \bar{t}}>) = \argmax\limits_r \text{Re}(<{\bf t}, {\bf r}, {\bf \bar{h}}>) = {\bf r}_1 r 2 = r arg max Re ( < h , r , t ˉ > ) = r arg max Re ( < t , r , h ˉ > ) = r 1
ComplEx share the same property with DistMult
Cannot possible Composition relations
Can possible 1-to-N relations
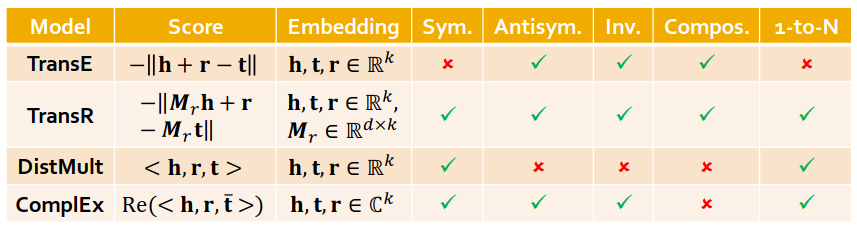
KG Embeddings in Practice#
Different KGs may have drastically different relation patterns!
There is not a general embedding that works for all KGs, use the table to select models
Try TransE for a quick run if the target KG does not have much symmetric relations
Then use more expressive models, e.g., ComplEx, RotatE (TransE in Complex space)
📌 Link prediction / Graph completion is one of the prominent tasks on knowledge graphs
Mark
A linear layer is a type of neural network layer that performs a linear transformation of the input vector, which is often used to transform the input vector into a higher-dimensional space. This transformation can be thought of as defining a hyperplane in the new space that separates the input vectors into two regions.