This post based on Lecture 11 of CS224W

Reasoning over Knowledge Graphs#

Goal:

• How to perform multi-hop reasoning over KGs?

Reasoning over Knowledge Graphs

• Answering multi-hop queries
  • Path Queries
  • Conjunctive Queries
• Query2Box

Predictive Queries on KG#

Can we do multi-hop reasoning, i.e., answer complex queries on an incomplete, massive KG?

KG completion: Is link $(h, r, t)$ in the KG?

One-hop Queries#

One-hop query: Is $t$ an answer to query $(h, r)$?

• For example:
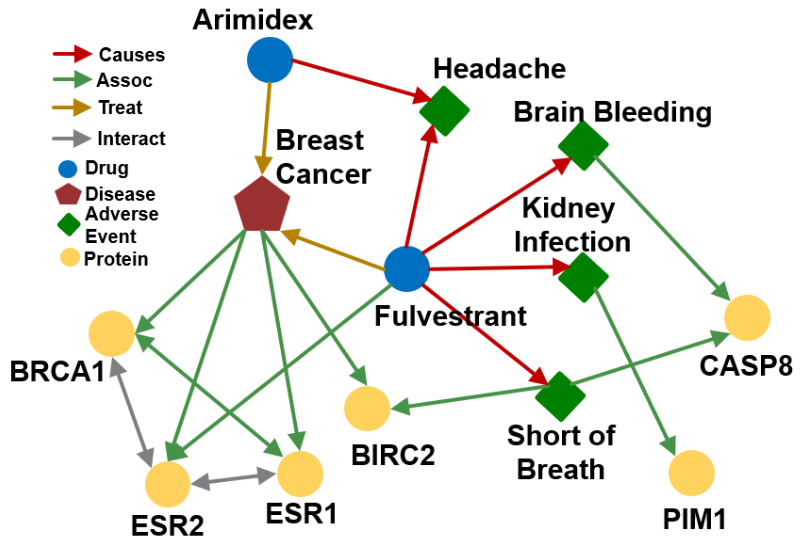
  • Q: What side effects are caused by drug Fulvestrant?
  • A: [Headache, Brain Bleeding, Kidney Infection, Short of Breath]

Path Queries#

Generalize one-hop queries to path queries by adding more relations on the path.

An $n$-hop path query $q$ can be represented by $q = (v_a ,(r_1, ..., r_n ))$

• $v_a$ is an “anchor” entity,
• Let answers to $q$ in graph $G$ be denoted by ${\llbracket q \rrbracket}_G$.

Query Plan of $q$:

Query plan of path queries is a chain.

• For example:
  • Q: “What proteins are associated with adverse events caused by Fulvestrant?”
  • A: [BIRC2, CASP8, PIM1]

$v_a$ is $e$:Fulvestrant

$(r_1, r_2)$ is ($r$:Causes, $r$:Assoc)

Query: ($e$:Fulvestrant, ($r$:Causes, $r$:Assoc))

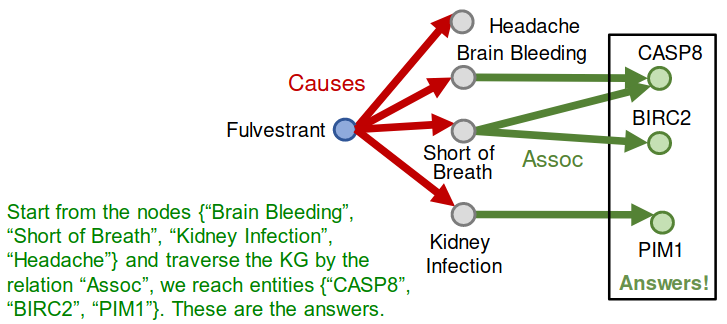
• Answering queries seems easy: Just traverse the graph.
• But KGs are incomplete and unknown:
  • For example, we lack all the biomedical knowledge
  • Enumerating all the facts takes non-trivial time and cost, we cannot hope that KGs will ever be fully complete
• Due to KG incompleteness, one is not able to identify all the answer entities

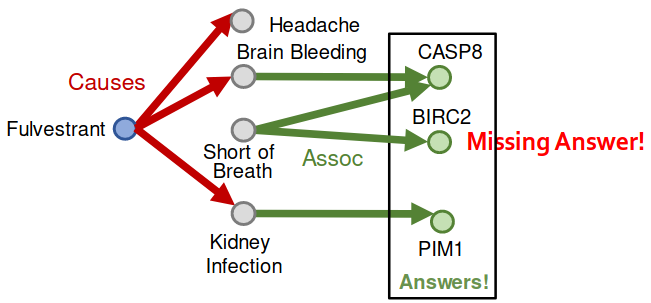
위의 그래프와 비교하면 Fulvestrant와 Short of Breath의 Causes relation이 없다. 이로 인해 BIRC2라는 단백질에 대하여 정상적인 relation을 찾기 어렵다.

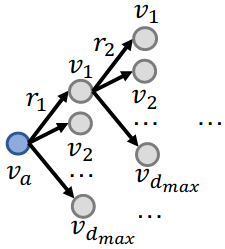
Can we first do KG completion and then traverse the completed (probabilistic) KG?

• No! The “completed” KG is a dense graph!
  • Most $(h, r, t)$ triples (edge on KG) will have some non-zero probability.
• Time complexity of traversing a dense KG is exponential as a function of the path length $L$: ${\cal O}(d_{max}^L)$

Answering Predictive Queries on Knowledge Graphs#

Predictive Queries#

We need a way to answer path-based queries over an incomplete knowledge graph.

We want our approach to implicitly impute and account for the incomplete KG.

• Want to be able to answer arbitrary queries while implicitly imputing for the missing information
• Generalization of the link prediction task

1. Given entity embeddings, how do we answer an arbitrary query?

   1. Path queries: Using a generalization of TransE
   2. Conjunctive queries: Using Query2Box
   3. And-Or Queries: Using Query2Box and query rewriting

   (We will assume entity embeddings and relation embeddings are given)

2. How do we train the embeddings?

   1. The process of determining entity and relation embeddings which allow us to embed a query.

General Idea#

Map queries into embedding space. Learn to reason in that space

• Embed query into a single point in the Euclidean space: answer nodes are close to the query.
• Query2Box: Embed query into a hyper-rectangle (box) in the Euclidean space: answer nodes are enclosed in the box.

Guu, et al., Traversing knowledge graphs in vector space, EMNLP 2015.

Key idea: Embed queries!

• Generalize TransE to multi-hop reasoning.

Recap: TransE: Translate ${\bf h}$ to ${\bf t}$ using ${\bf r}$ with score function $f_r(h, t) = −\| {\bf h} + {\bf r} − {\bf t}\|$.

Another way to interpret this is that:

• Query embedding: ${\bf q} = {\bf h} + {\bf r}$

• Goal: query embedding ${\bf q}$ is close to the answer embedding ${\bf t}$

  $f_q(t)=-\|{\bf q} - {\bf t}\|$

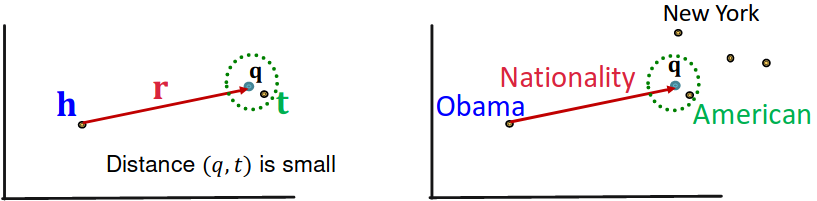
Given a path query $q = (v_a, (r_1, ... , r_n))$,

${\bf q} = {\bf v}_a + {\bf r_1} + \cdots + {\bf r_n}$

The embedding process only involves vector addition, independent of # entities in the KG!

• Q: “What proteins are associated with adverse events caused by Fulvestrant?”
• A: [BIRC2, CASP8, PIM1]

Query: ($e$:Fulvestrant, ($r$:Causes, $r$:Assoc))

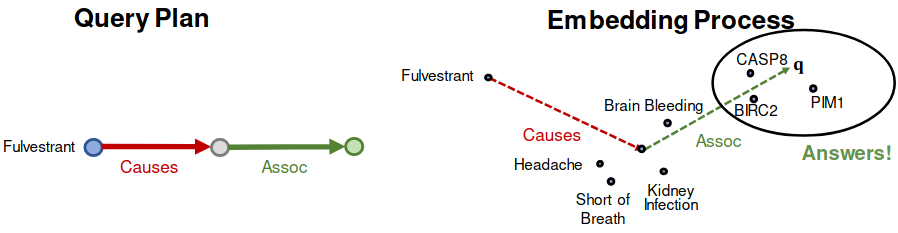
TransE는 path query 처리가 가능하다. compositional relations이 가능하기 때문이다.

TransR / DistMult / ComplEx는 path query 처리에 어려움이 있다.

TransR 역시 compositional relations이 가능하지만, relation들 간의 직접적인 연관아 아니라 projection matrix를 거쳐야 해서 path query 처리가 힘들어 사용하지 않는다.

Conjunctive Queries#

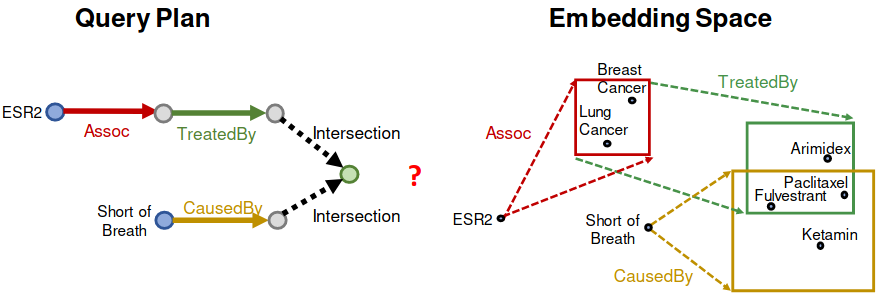
Q: “What are drugs that cause Short of Breath and treat diseases associated with protein ESR2?”

A: [”Fulvestrant”]

(($e$: ESR2, ($r$: Assoc, $r$: TreatedBy)), ($e$: Short of Breath, ($r$: CausedBy))

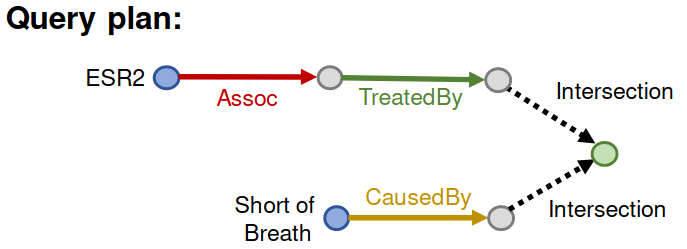
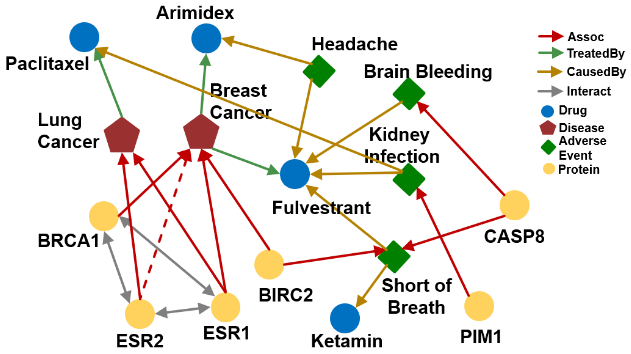
Following the graph, ESR2’s associate relation is missing. Thus, we can’t find Fulvestrant.

How can we use embeddings to implicitly impute the missing (ESR2, Assoc, Breast Cancer)?

Intuition: ESR2 interacts with both BRCA1 and ESR. Both proteins are associated with breast cancer.

How can we answer more complex queries with logical conjunction operation?

1. Each intermediate node represents a set of entities, how do we represent it?
2. How do we define the intersection operation in the latent space?

Query2Box#

Ren et al., Query2box: Reasoning over Knowledge Graphs in Vector Space Using Box Embeddings, ICLR 2020

Embed queries with hyper-rectangles (boxes)

• ${\bf q} = (\text{Center}(q), \text{Offset}(q))$

Boxes are a powerful abstraction, as we can project the center and control the offset to model the set of entities enclosed in the box

$d$: out degree

$|V|$: # entities

$|R|$: # relations

Things to figure out:

• Entity embeddings (# params: $d|V|$):
  • Entities are seen as zero-volume boxes
• Relation embeddings (# params: $2d|R|$):
  • Each relation takes a box and produces a new box
• Intersection operator $f$:
  • New operator, inputs are boxes and output is a box
  • Intuitively models intersection of boxes

Q: “What are drugs that cause Short of Breath and treat diseases associated with protein ESR2?”

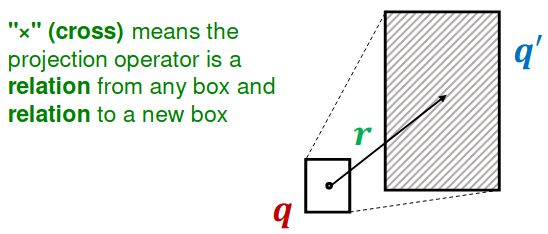
Projection Operator $\cal P$#

Intuition:

• Take the current box as input and use the relation embedding to project and expand the box!

${\cal P}: \text{Box} \times \text{Relation} \rarr \text{Box}$

$\begin{aligned}
{\bf q'} &= (\text{Center}(q'), \text{Offset}(q'))\\
\text{Cen}(q') &= \text{Cen}(q) + \text{Cen}(r)\\
\text{Off}(q') &= \text{Off}(q) + \text{Off}(r)\\
\end{aligned}$

Geometric Intersection Operator $\cal J$#

Take multiple boxes as input and produce the intersection box

Intuition:

• The center of the new box should be “close” to the centers of the input boxes
• The offset (box size) should shrink (since the size of the intersected set is smaller than the size of all the input set)

${\cal J}: \text{Box} \times \cdots \times \text{Box} \rarr \text{Box}$

$\text{Cen}(q_\text{inter})
 = \sum_i {\bf w}_i \odot \text{Cen}(q_i)\\
{\bf w}_i = \frac{\exp(f_\text{cen}(\text{Cen}(q_i)))}{\sum_j\exp(f_\text{cen}(\text{Cen}(q_i)))}$

$\text{Cen}(q_i) \in {\Bbb R}^d$

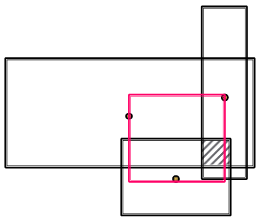
${\bf w}_i \in {\Bbb R}^d$: trainable weights are calculated by a neural network $f_\text{cen}$; represents a “self-attention” score for the center of each input $\text{Cen}(q_i)$.

Intuition: The center should be in the red region!

Implementation: The center is a weighted sum of the input box centers

$\text{Off}(q_\text{inter})
 = \min\left(\text{Off}(q_1), ..., \text{Off}(q_n)\right) \odot \sigma\left(f_\text{off}(\text{Off}(q_1), ..., \text{Off}(q_n))\right)$

$\min\left(\text{Off}(q_1), ..., \text{Off}(q_n)\right)$: guarantees shrinking

$f_\text{off}$: a neural network that extracts the representation of the input boxes to increase expressiveness

$\sigma$: Sigmoid function (0, 1); $\frac{1}{1+\exp(−x)}$

Intuition: The offset should be smaller than the offset of the input box

Implementation: We first take minimum of the offset of the input box, and then we make the model more expressive by introducing a new function $f_\text{off}$ to extract the representation of the input boxes with a sigmoid function to guarantee shrinking.

Entity-to-Box Distance#

How do we define the score function $f_q(v)$ (negative distance)?
($f_q(v)$ captures inverse distance of a node $v$ as answer to $q$)

Given a query box ${\bf q}$ and entity embedding (box) ${\bf v}$,

$\begin{aligned}
{\bf q}_\text{max} &= \text{Cen}({\bf q}) + \text{Off}({\bf q}) \in {\Bbb R}^d \\
{\bf q}_\text{min} &= \text{Cen}({\bf q}) - \text{Off}({\bf q}) \in {\Bbb R}^d\\
d_\text{out}({\bf q}, {\bf v}) &= \|\max({\bf v} - {\bf q}_\text{max} , {\bf 0}) + \max({\bf q}_\text{min} - {\bf v}, {\bf 0})\|_1,\\
d_\text{in}({\bf q}, {\bf v}) &= \|\text{Cen}({\bf q}) - \min({\bf q}_\text{max},\max({\bf q}_\text{min}, {\bf v}))\|_1,\\
d_\text{box}({\bf q}, {\bf v}) &= d_\text{out}({\bf q}, {\bf v}) + \alpha\cdot d_\text{in}({\bf q}, {\bf v})\\
f_q(v) &= -d_\text{box}({\bf q}, {\bf v})
\end{aligned}$

where $0 < \alpha < 1$.

${\bf q} \in {\Bbb R}^{2d}$: a query box

${\bf v} \in {\Bbb R}^{d}$: an entity vector

$d$: the distance

Intuition: if the point is enclosed in the box, the distance should be downweighted.

• Examples:
  $\alpha$ is 0.5.
  • 1 + 0.5(3) = 2.5; $v$ outside the box $\rarr f_q(v)$ = -2.5
  • 0 + 0.5(3) = 1.5; $v$ at the line of the box $\rarr f_q(v)$ = -1.5
  • 0 + 0.5(1) = 0.5; $v$ in the box $\rarr f_q(v)$ = -0.5

Union Operation#

Can we embed complex queries with union?
(e.g.: “What drug can treat breast cancer or lung cancer?”)

Conjunctive queries + disjunction is called Existential Positive First-Order (EPFO) queries.

We’ll refer to them as AND-OR queries.

Can we also design a disjunction operator and embed AND-OR queries in low-dimensional vector space?

• No! Intuition: Allowing union over arbitrary queries requires high-dimensional embeddings!

Given 3 queries $q_1$, $q_2$, $q_3$, with answer sets:

• $\llbracket q_1\rrbracket = \{v_1\}$, $\llbracket q_2\rrbracket = \{v_2\}$, $\llbracket q_3\rrbracket = \{v_3\}$
• If we allow union operation, can we embed them in a two-dimensional plane?

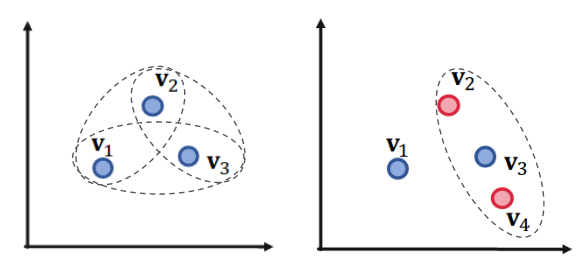
If given 4 queries $q_1$, $q_2$, $q_3$, $q_4$ with answer sets:

• We cannot design a box embedding for $q_2 \lor q_4$, that only $v_2$ and $v_4$ are in the box but $v_3$ is in the box.

Conclusion: Given any $M$ conjunctive queries $q_1, ... , q_M$ with non-overlapping answers, we need dimensionality of $\Theta(M)$ to handle all OR queries.

• For real-world KG, such as FB15k, we find $M \geq 13,365$, where $|V| = 14,951$.
• Remember, this is for arbitrary OR queries.

Can’t we still handle them?

Key idea: take all unions out and only do union at the last step!

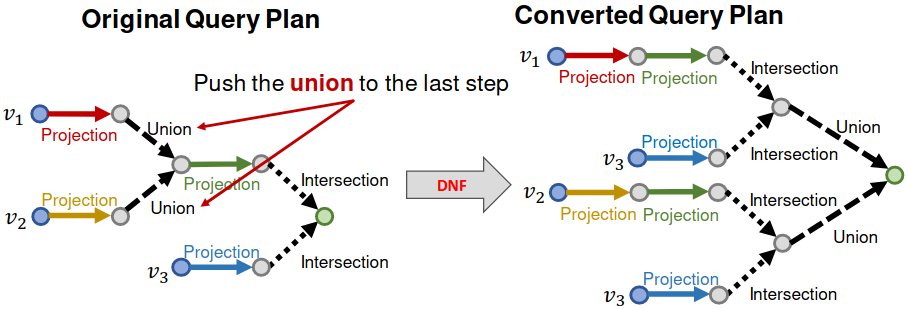
Disjunctive Normal Form#

Any AND-OR query can be transformed into equivalent DNF, i.e., disjunction of conjunctive queries.

Given any AND-OR query $q$,

$q = q_1 \lor q_2 \lor \cdots \lor q_m$. where $q_i$ is a conjunctive query.

Now we can first embed each $q_i$ and then “aggregate” at the last step!

Distance between entity embedding and a DNF ($q = q_1 \lor q_2 \lor \cdots \lor q_m$) is defined as:

$d_\text{box}({\bf q}, {\bf v}) = \min(d_\text{box}({\bf q}_1, {\bf v}), ..., d_\text{box}({\bf q}_m, {\bf v}))$

Intuition:

• As long as $v$ is the answer to one conjunctive query $q_i$, then $v$ should be the answer to $q$
• As long as ${\bf v}$ is close to one conjunctive query ${\bf q}_i$,then ${\bf v}$ should be close to ${\bf q}$ in the embedding space

The process of embedding any AND-OR query $q$:

1. Transform $q$ to equivalent DNF $q_1 \lor \cdots \lor q_m$
2. Embed $q_1$ to $q_m$
3. Calculate the (box) distance $d_\text{box}({\bf q}_i, {\bf v})$
4. Take the minimum of all distance
5. The final score $f_q(v) = -d_\text{box}({\bf q}, {\bf v})$

How to Train Query2Box#

Overview and Intuition (similar to KG completion):

Given a query embedding ${\bf q}$, maximize the score $f_q(v)$ for answers $v \in \llbracket q \rrbracket$ and minimize the score $f_q(v^\prime)$ for negative answers $v^\prime \notin \llbracket q \rrbracket$

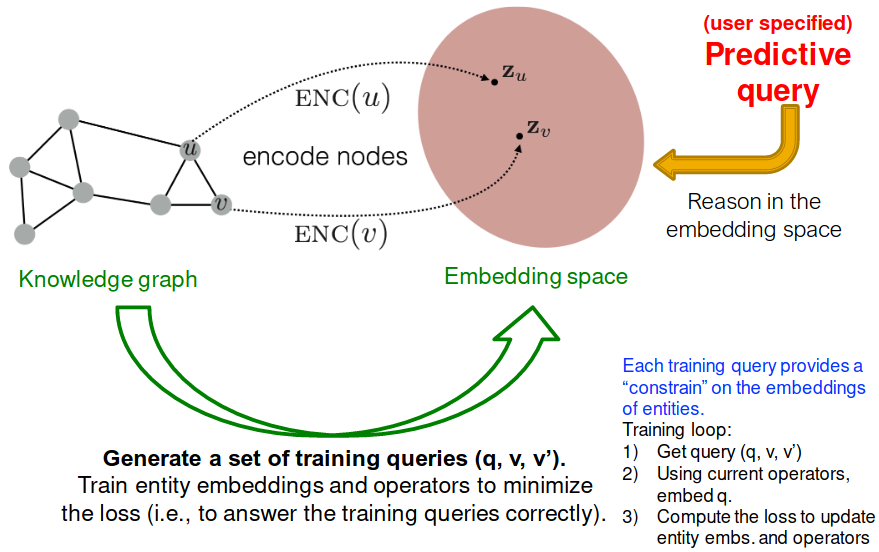
Training:

1. Sample a query $q$ from the training graph $G_\text{train}$, answer $v \in \llbracket q \rrbracket_{G_\text{train}}$, and non-answer $v^\prime \notin \llbracket q \rrbracket_{G_\text{train}}$
2. Embed the query ${\bf q}$.
   • Use current operators, to compute query embedding.
3. Calculate the score $f_q(v)$ and $f_q(v^\prime)$.
4. Optimize embeddings and operators to minimize the loss ${\cal L}$ (maximize $f_q(v)$ while minimize $f_q(v^\prime)$:

   ${\cal L} = - \log\sigma(f_q(v)) - \log(1 - \sigma(f_q(v^\prime)))$